Seminars in March 2011

  • Yoomi Rho (노유미), L(j,k) Labelings of Direct Product of Complete Graphs
    L(j,k) labelings of direct product of complete graphs
    Yoomi Rho (노유미)
    Dept. of Mathematics, Univ. of Incheon, Incheon, Korea.
    2011/3/17 Thu 4:30PM-5:30PM (E6-1, Room 3433)
    An L(j,k) labeling of a graph is a vertex labeling such that the difference of the labels of any two adjacent vertices is at least j and that of any two vertices of distance 2 is at least k. The minimum of the spans of all L(j,k)-labelings of G is denoted by 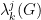\lambda_k^j(G). Recently Haque and Jha proved if G is a direct product of complete graphs, then 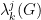\lambda_k^j(G) coincide with the trivial lower bound $(N-1)k$ where N is the order of G when j/k is within a certain bound.</p>

    In this paper, we suggest a new labeling method of such a graph G. With this method, we extend the range of j/k such that \lambda_k^j(G)=(N-1)k holds. Moreover, we obtain an upper bound of \lambda_k^j(G) for the remaining cases.

    Tags:

  • Seog-Jin Kim (김석진), Decomposition of Sparse Graphs into Forests and a Graph with Bounded Degree
    Decomposition of Sparse Graphs into Forests and a Graph with Bounded Degree
    Seog-Jin Kim (김석진)
    Dept. of Mathematics Education, Konkuk University, Seoul, Korea.
    2011/3/10 Thu 5PM-6PM
    Say that a graph with maximum degree at most d is d-bounded. For d>k, we prove a sharp sparseness condition for decomposability into k forests and a d-bounded graph. Consequences ar e that every graph with fractional arboricity at most k+ d/(k+d+1) has such a decomposition, and (for k=1) every graph with maximum average degree less than 2+2d/(d+2) decomposes into a forest and a d-bounded graph. When d=k+1, and when k=1 and d≤6, the d-bounded graph in the decomposition can also be required to be a forest. When k=1 and d≤2, the d-bounded forest can also be required to have at most d edges in each component.
    This is joint work with A.V. Kostochka, D.B. West, H. Wu, and X. Zhu.
    Tags:

Monthly Archives