Finding a spanning Halin subgraph in 3-connected  -free graphs
-free graphs
Suil O
Georgia State University, USA
Georgia State University, USA
2014/08/28 *Thursday* 4PM-5PM
Room 1409
Room 1409
A Halin graph is constructed from a plane embedding of a tree whose non-leaf vertices have degree at least 3 by adding a cycle through its leaves in the natural order determined by the embedding. In this talk, we prove that every 3-connected  -free graph has a spanning Halin subgraph. This result is best possible in the sense that the statement fails if
-free graph has a spanning Halin subgraph. This result is best possible in the sense that the statement fails if 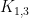 is replaced by
is replaced by  or
or  is replaced by
is replaced by 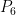 . This is a joint work with Guantao Chen, Jie Han, Songling Shan, and Shoichi Tsuchiya.
. This is a joint work with Guantao Chen, Jie Han, Songling Shan, and Shoichi Tsuchiya.